fibonacci archivos -

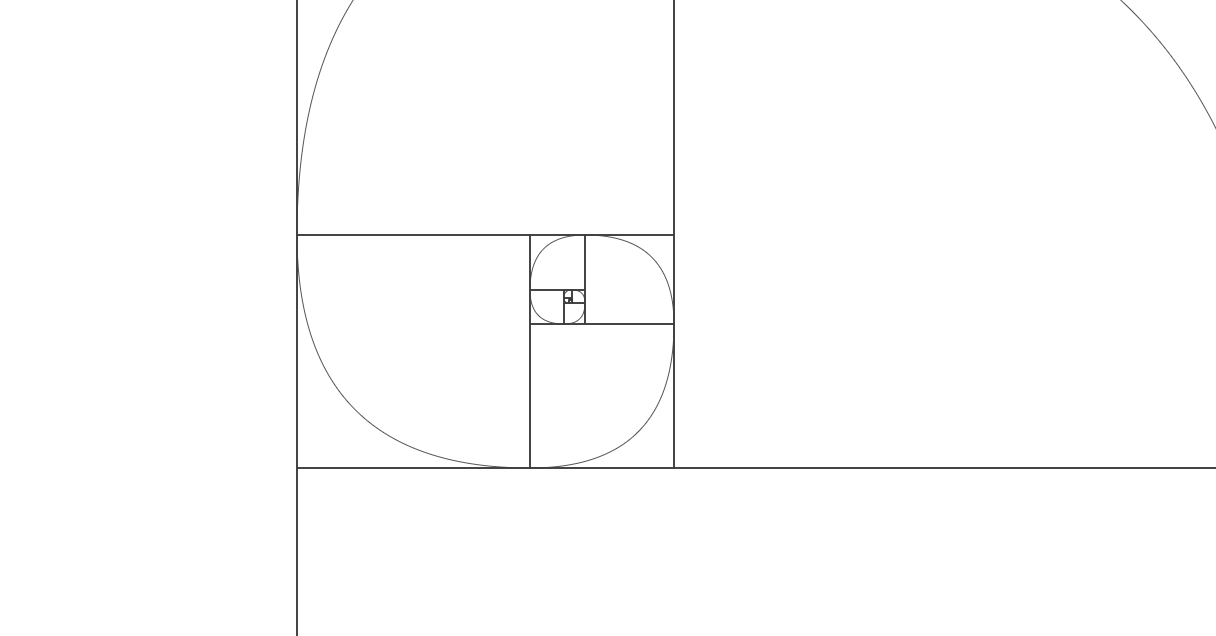
Como vimos en un articulo que publique anteriormente (función fibonacci en javascript), la secuencia fibonacci es una curiosidad de la naturaleza y una de las cuales vemos en carreras afines a ingeniería, y en esta entrada compartiré el código fuente de la representación mas conocida de dicha secuencia, el caracol.

Esta figura es la mas conocida cuando buscamos información sobre la secuencia fibonacci, y pueden ver el algoritmo en ejecución dando clic AQUÍ.

El siguiente código de javascript la muestra en un navegador que soporte HTML5 (por la utilización de canvas):

Código HTML

<!DOCTYPE html PUBLIC "-//W3C//DTD XHTML 1.0 Transitional//EN" "http://www.w3.org/TR/xhtml1/DTD/xhtml1-transitional.dtd">
<html xmlns="http://www.w3.org/1999/xhtml">
<head>
<meta http-equiv="Content-Type" content="text/html; charset=utf-8" />
<title>fibonacci cuadros</title>
<style>
* { margin:0; padding:0; }
html, body { width:100%; height:100%; }
#miCanvas {
position: absolute;
top: 0px;
left: 0px;

margin: 0px;
border:1px solid #333
}
</style>
</head>

<body>
<canvas id="miCanvas"    ></canvas>
</body>
</html>

Código Javascript

/*
Código realizado por: Héctor de León Guevara.
Fecha: 06/04/2014
Figura caracol con secuencia fibonacci
www.hdeleon.net
*/

var context //contexto del canvas global
//variables para el acomodo
var x=700;
var y=300;
var opcion=0 //variable que indica cual es la posicion ue sigue para dibujar el cuadro
var opcionCurva=0; //variable de opcion para la curva

//variables de curva
var x1_curva;
var y1_curva;
var x2_curva;
var y2_curva;
var x3_curva;
var y3_curva;

//inicia el script
window.onload = function() {
//creamos canvas
var canvas = document.getElementById('miCanvas');
context = canvas.getContext('2d');

//agrega event de resize
window.addEventListener('resize', resizeCanvas, false);

//redimensiona canvas al tamaño de ventana
function resizeCanvas() {
canvas.width = window.innerWidth;
canvas.height = window.innerHeight;
}
//redimencionamos canvas
resizeCanvas();

//algoritmos fibonacci, se ejecuta 40 veces
fibonacci(40)

};

function fibonacci(n){
var a=0;
var b=1;
var numeroTemporal=a

//plasmaCuadro(x,y,b,b);
for(i=0; i<n;i++){

acomodaCuadro(a,b);

numeroTemporal=a;
a=b;
b=numeroTemporal+b;

acomodaCurva(a,b);
//dibujamos cuadro
plasmaCuadro(x,y,b,b);
plasmaCurva();
}
}
function plasmaCurva(){
//curva
context.moveTo(x1_curva,y1_curva); //mover el cursor de canvas a punto inicial
context.quadraticCurveTo(x2_curva,y2_curva,x3_curva,y3_curva);	//punto de cuadricula y punto final
context.strokeStyle = '#555';
context.stroke();
}

function plasmaCuadro(x,y,w,h){
context.beginPath();
context.rect(x, y,w, h);

context.lineWidth = 1;
context.strokeStyle = 'black';

context.stroke();
}

//funcion que permite ir acomodando el cuadro para que figure el espiral
function acomodaCuadro(a,b){
switch(opcion){
//inicio
case 0:
opcion++;
break;
//derecha
case 1:
x+=b;

opcion++;
break;
//abajo
case 2:
x-=a;
y+=b;
opcion++;
break;
//izquierda
case 3:
x-=(parseInt(a)+parseInt(b));
y-=a;
opcion++;
break;
//arriba
case 4:

y-=(parseInt(a)+parseInt(b));
opcion++;
break;
}

if(opcion==5)
opcion=1;
}

function acomodaCurva(a,b){
switch(opcionCurva){

//derecha
case 1:
x1_curva=x;
y1_curva=y;
x2_curva=x+b;
y2_curva=y;
x3_curva=x+b;
y3_curva=y+b;
break;
//abajo
case 2:
x1_curva=x+b;
y1_curva=y;
x2_curva=x+b;
y2_curva=y+b;
x3_curva=x;
y3_curva=y+b;
break;
//izquierda
case 3:
x1_curva=x+b;
y1_curva=y+b;
x2_curva=x;
y2_curva=y+b;
x3_curva=x;
y3_curva=y;
break;
//arriba
case 4:
x1_curva=x;
y1_curva=y+b;
x2_curva=x;
y2_curva=y;
x3_curva=x+b;
y3_curva=y;
break;
}
opcionCurva++;

if(opcionCurva==5)
opcionCurva=1;
}

La secuencia de fibonacci es un algoritmo tipico que vemos todos los ingenieros de computación (o ciencia a fin), mientras estamos cursando nuestra carrera.

Esta Sucesión es muy simple de comprender, simplemente comienza por el número 0 seguido del 1, y a partir de estos se suma cada numero con el anterior y se agrega a la secuencia, y repetimos la operación; un ejemplo es el siguiente:

0,1,1,2,3,5,8,13…..

Lo interesante es que esta función se representa en muchos casos en la naturaleza, desde la perfección de un caracol, hasta en la reproducción de los conejos; gran ejemplo que nos hace pensar que la naturaleza es un gran matemático.

Les adjunto el código de javascript para realizar esta famosa secuencia a continuación:

function fibonacci(n){
var a=0;
var b=1;

for(i=0; i<n;i++){
var numeroTemporal=a;
a=b;
b=numeroTemporal+b;

document.writeln(a+" ");
}

}

Esta función recibe un número, el cual sera la cantidad de elementos que plasmara la función. Si desean ver en acción la función les anexo el código corriendo el cual plasma los primeros 100 números de la secuencia, solo den clic en el botón de abajo:

Etiqueta: fibonacci

Solución a Fibonacci y Factorial con Programación Funcional

Caracol Fibonacci en javascript. #fibonacci #canvas #javascript

Función #Fibonacci en #javascript